15 calc questions

/in /by

15 calc questions

1.

If f(x) is differentiable for the closed interval [-3, 2] such that f(-3) = 4 and f(2) = 4, then there exists a value c, -3 < c < 2 such that (4 points)


2.

If f(x) = ι(x2 – 8)ι, how many numbers in the interval 0 ≤ x ≤ 2.5 satisfy the conclusion of the mean value theorem? (4 points)



3.

Find the exact value of the following limit: 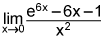the limit as x goes to 0 of the quotient of the quantity e raised to the 6 times x power minus 6 times x minus 1 and x squared . (4 points)




4.

For which pair of functions f(x) and g(x) below will the 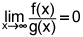limit as x goes to infinity of the quotient of f of x and g of x equals 0 ? (4 points)



5.

Evaluate 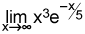the limit as x goes to infinity of the product of x cubed and e raised to the power of negative x over 5 . (4 points)

1.

Which of the following is the best linear approximation for f(x) = tan(x) near 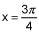x equals 3 times pi divided by 4 ? (4 points)


2.

If f(2) = 10 and 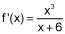f prime of x equals the quotient of x cubed and the quantity x plus 6 , which of the following is the best approximation for f(2.03) using local linearization? (4 points)



3.

The function’s value will always be greater than or equal to the local linear approximation of a function f if, for all x in an interval containing the point of tangency, (4 points)



4.

At the point of tangency, the function’s value and the local linear approximation of a function have the same value. (4 points)



5.

If f is a function such that 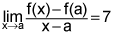the limit as x approaches a of the quotient of the quantity f of x minus f of a and the quantity x minus a equals 7 , then which of the following statements must be true? (4 points)

Last 5 must SHOW ALL WORK

Let g be a function that is defined for all x, x ≠ 2, such that g(3) = 4 and the derivative of g is
g′(x) = quotient of quantity x squared minus sixteen and x minus two with x ≠ 2.

  1. Find all values of x where the graph of g has a critical value.
  2. For each critical value, state whether the graph of g has a local maximum, local minimum, or neither. You must justify your answers with a complete sentence.
  3. On what intervals is the graph of g concave down? Justify your answer.
  4. Write an equation for the tangent line to the graph of g at the point where x = 3.
  5. Does this tangent line lie above or below the graph at this point? Justify your answer.