Multiple Choice Calc

/in /by

Multiple Choice Calc

1.

Describe how the graph of y = x4 can be transformed to the graph of the given equation.

y = (x – 5)4 (5 points)


2.

Use your calculator and a table of values to find the exact value of 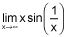limit as x goes to infinity of the product of x and the sine of 1 over x . (The limit as x approaches infinity) (5 points)




3.

Use the graph below to evaluate 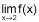the limit as x approaches 2 of f of x :

Graph of a function that increases for x greater than or equal to 0 and less than 2 and decreases for x greater than 2 and less than or equal to 4. The point 2, 3 is marked on the graph (5 points)



4.

Find the vertical asymptote(s) for the function 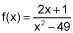the quotient of the quantity 2 times x plus 1 and the quantity x squared minus 49 . (5 points)



5.

The end behavior of 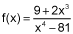f of x equals the quotient of the quantity 9 plus 2 times x cubed and the quantity x to the 4th power minus 81 most closely matches which of the following? (5 points)



6.

Which of the following functions is continuous at x = 2? (5 points)



7.

Evaluate 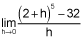the limit as h goes to 0 of the quotient of the quantity the 5th power of 2 plus h minus 32 and h . (5 points)



8.

Find f ‘(x) for f(x) = 8x3 + 2x2 – 8x + 10. (5 points)



9.

Find g ‘(x) for g(x) = sin(6x). (5 points)



10.

Where is the second derivative of y = 3xe-x equal to 0? (5 points)



11.

If f(x) = arcsin(2x), then f ‘(x) = ? (5 points)



12.

The graph of the derivative, f ‘(x) is shown below. On what interval is the graph of f (x) increasing?

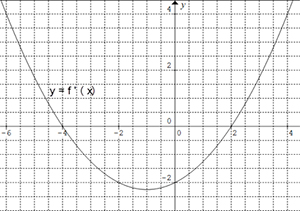graph is a parabola with x intercepts at x equals negative 4 and 2 and y intercept at y equals negative 2 (5 points)



13.

A particle moves along the x-axis with position function s(t) = esin(x). How many times in the interval [0, 2π] is the velocity equal to 0? (5 points)



14.

An ice block is melting so that the length of each side is changing at the rate of 1.5 inches per hour. How fast is the surface area of the ice cube changing at the instant the ice block has a side length of 2 inches? (5 points)



15.

Use the graph of f(x) = |x(x2 – 1)| to find how many numbers in the interval [0.5, 0.75] satisfy the conclusion of the Mean Value Theorem. (5 points)