Function solutions
This week we are learning about rational functions, and the discussion this week shows how you can use a rational function to determine how much your monthly phone bill will be.
These days when you get a new contract you have the choice to pay the phone up front, or to pay for it over the course of your contract. The total you pay for 2 years depends on which method you choose.
Pay up front: Total = phone + (monthly bill)(24)
How does the phone company figure out how much you’d pay monthly if you do it in installments? Well they do the following:
Pay in monthly installments = Total/24
We can generalize that equation to find the monthly bill as
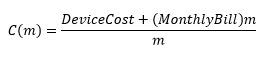
If you plan on paying your phone off in 1 year, use m=12 (12 months) to find out how much you’d pay a month. If you want to pay it off after 2, pick m=24.
For this discussion you are to do the following:
- Give the function C(m), doing research to determine numbers for the Device Cost and the Monthly Bill.
- Find the asymptotes (horizontal and vertical)
- Tell us what smallest monthly cost you can get the bill down to, and explain how you determined that.
- Find out the average cost (i.e. the overall monthly bill) if you plan to pay the phone off in 2 years.
- Reflect on this monthly cost. Does this make you reconsider the price of the phone you want to buy (i.e. maybe get a cheaper phone, or you have the money in your budget to spend more).


