8 short answer calc

/in /by

8 short answer calc

Answer in WORD doc. please

1.

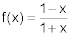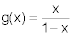For f of x equals the quotient of the quantity 1 minus x and the quantity 1 plus x and g of x equals the quotient of the quantity x and the quantity 1 minus x , find the simplified form for f [g(x)] and state the domain.

2.

Evaluate 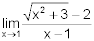the limit as x approaches 1 of the quotient of the square root of the quantity x squared plus 3 minus 2 and the quantity x minus 1 . You must show your work to receive credit.

3.

A particle moves on a line away from its initial position so that after t hours it is s = 6t2 + 2t miles from its initial position. Find the average velocity of the particle over the interval [1, 4]. Include units in your answer.

4.

Use the table below to evaluate 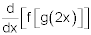the derivative with respect to x of g of f of 2 times x at x = 1.

x 1 2 3 4
f(x) 6 1 8 2
f ‘(x) 6 1 8 2
g(x) 1 4 4 3
g ‘(x) 9 5 5 -4

5.

Find the x-coordinates where f ‘(x) = 0 for f(x) = 2x + sin(4x) in the interval [0, π].

6.

Find 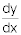dy over dx for 4 – xy = y3. You must show your work to receive credit.

7.

A 120-inch strip of metal 12 inches wide is to be made into a small open trough by bending up two sides on the long side, at right angles to the base. The sides will be the same height, x. If the trough is to have a maximum volume, how many inches should be turned up on each side?

8.

The radius of a 12 inch right circular cylinder is measured to be 4 inches, but with a possible error of ±0.2 inch. Use linear approximation or differentials to determine the possible error in the volume of the cylinder. Include units in your answer.