15 Multiple Choice Calculus
1.
Which of the following integrals represents the area of the region bounded by x = e and the functions f(x) = ln(x) and g(x) = log1/e(x)? (4 points)
2.
Which integral gives the area of the region in the first quadrant bounded by the axes, y = ex, x = ey, and the line x = 4? (4 points)
3.
Find the area of the region bounded by the graphs of y = x2 – 4x and y = x – 4. (4 points)
4.
Find the area of the region bounded by the graphs of y = x, y = 4 – 3x, and x = 0. (4 points)
5.
Find the number a such that the line x = a divides the region bounded by the curves x = y2 − 1 and the y-axis into 2 regions with equal area. Give your answer correct to 3 decimal places. (4 points)
1.
Use your calculator to find the approximate volume in cubic units of the solid created when the region under the curve y = cos(x) on the interval [0,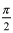 
] is rotated around the x-axis. (4 points)
2.
Find the volume of the solid formed by revolving the region bounded by the graphs of y = x3, x = 2, and y = 1 about the y-axis. (4 points)
3.
Which of the following integrals correctly computes the volume formed when the region bounded by the curves x2 + y2 = 25, x = 4 and y = 0 is rotated around the y-axis? (4 points)
4.
The base of a solid in the first quadrant of the xy plane is a right triangle bounded by the coordinate axes and the line x + y = 6. Cross sections of the solid perpendicular to the base are squares. What is the volume, in cubic units, of the solid? (4 points)
5.
The base of a solid in the region bounded by the two parabolas y2 = 8x and x2 = 8y. Cross sections of the solid perpendicular to the x-axis are semicircles. What is the volume, in cubic units, of the solid? (4 points)
1.
Find the average value of f(x)=e2x over the interval [2, 4]. (4 points)
2.
Find the velocity, v(t), for an object moving along the x-axis if the acceleration, a(t), is a(t) = cos(t) – sin(t) and v(0) = 3. (4 points)
3.
Find the distance, in feet, a particle travels in its first 2 seconds of travel, if it moves according to the velocity equation v(t)= 6t2 – 18t + 12 (in feet/sec). (4 points)
4.
For an object whose velocity in ft/sec is given by v(t) = -3t2 + 5, what is its displacement, in feet, on the interval t = 0 to t = 2 secs? (4 points)
5.
A pitcher throws a baseball straight into the air with a velocity of 72 feet/sec. If acceleration due to gravity is -32 ft/sec2, how many seconds after it leaves the pitcher’s hand will it take the ball to reach its highest point? Assume the position at time t = 0 is 0 feet. (4 points)
